Sorting

WHAT IS AN ALGORITHM?

The best definition of algorithms that I have come across is the following:

Algorithms are a series of steps or rules for solving a computational problem.

A computational problem is a collection of questions that computers might be able to solve.

An example of a simple algorithm could be one used by a coffee maker, it might look something like this:


	if (clock.getTime() == 7am){
		coffeMaker.boilWater();
		
		if(water.isBoiled()){
			coffeMaker.addCoffee();
			coffeMaker.pourCoffee();
		}
		
	} else{
		coffeMaker.doNothing();
	}

ALGORITHM EFFICIENCY

Algorithm efficiency is the study of the amount of resources used by an algorithm. The less resources used by the algorithm the more efficient it is. Nevertheless, to have a good comparison between different algorithms we can compare based on the resources it uses: how much time it needs to complete, how much memory it uses to solve a problem or how many operations it must do in order to solve the problem

Time efficiency: a measure of amount of time an algorithm takes to solve a problem.

Space efficiency: a measure of the amount of memory an algorithm needs to solve a problem.

Complexity theory: a study of algorithm performance based on cost functions of statement counts.

Bubble Sort

http://blogs.cuit.columbia.edu/zp2130/bubble_sort/
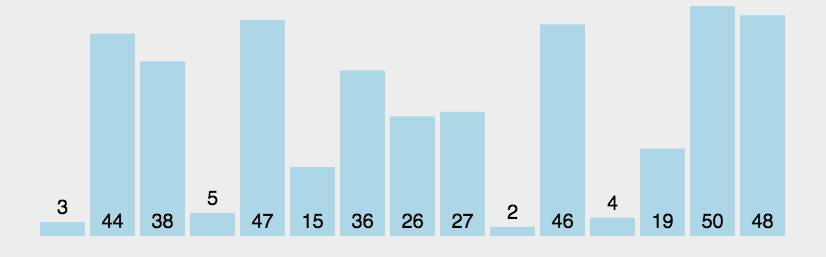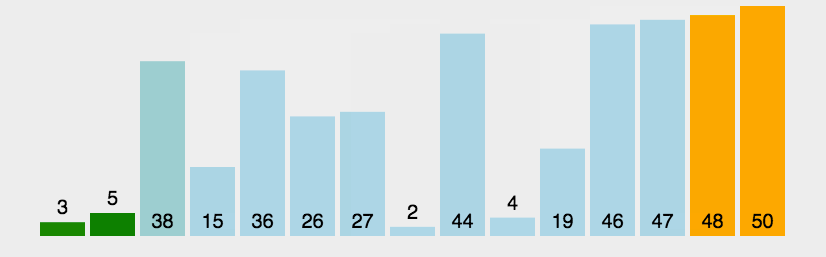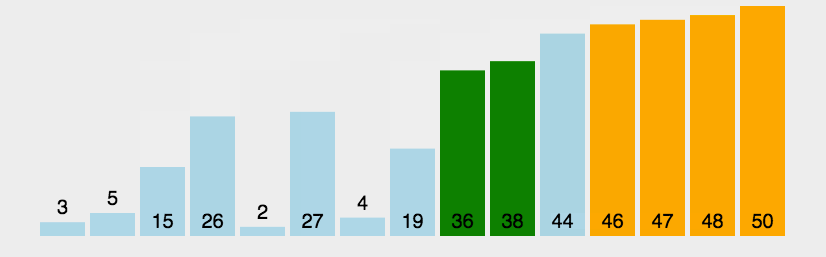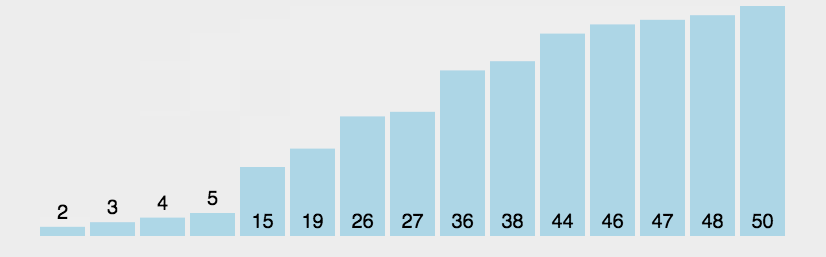
Selection Sort

http://blogs.cuit.columbia.edu/zp2130/selection_sort/
Insertion Sort

http://blogs.cuit.columbia.edu/zp2130/insertion_sort/
Shell Sort

http://blogs.cuit.columbia.edu/zp2130/shell_sort/
Merge Sort

http://blogs.cuit.columbia.edu/zp2130/merge_sort/
Quick Sort

http://blogs.cuit.columbia.edu/zp2130/quick-sort/
Heap Sort

http://blogs.cuit.columbia.edu/zp2130/heap_sort/
Counting Sort

http://blogs.cuit.columbia.edu/zp2130/counting_sort/
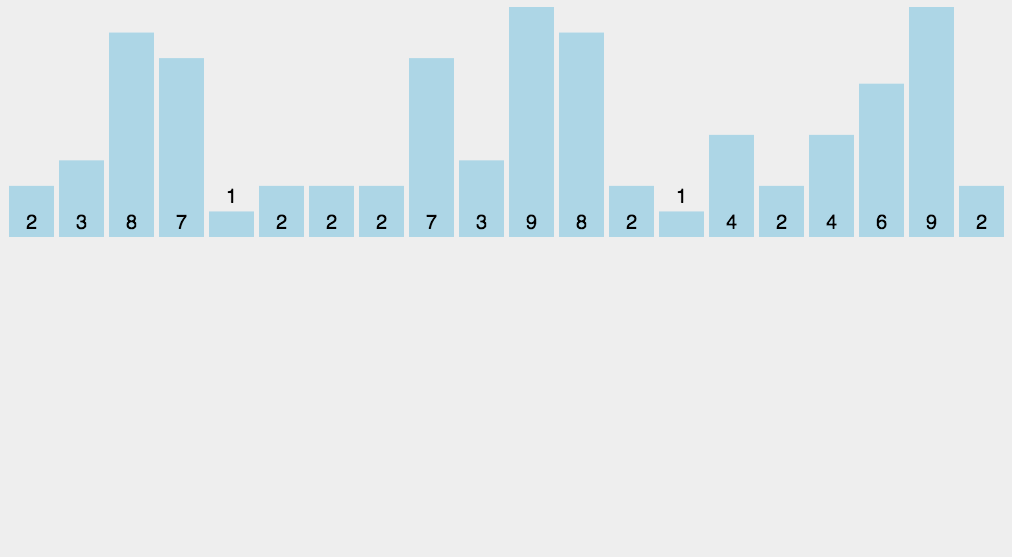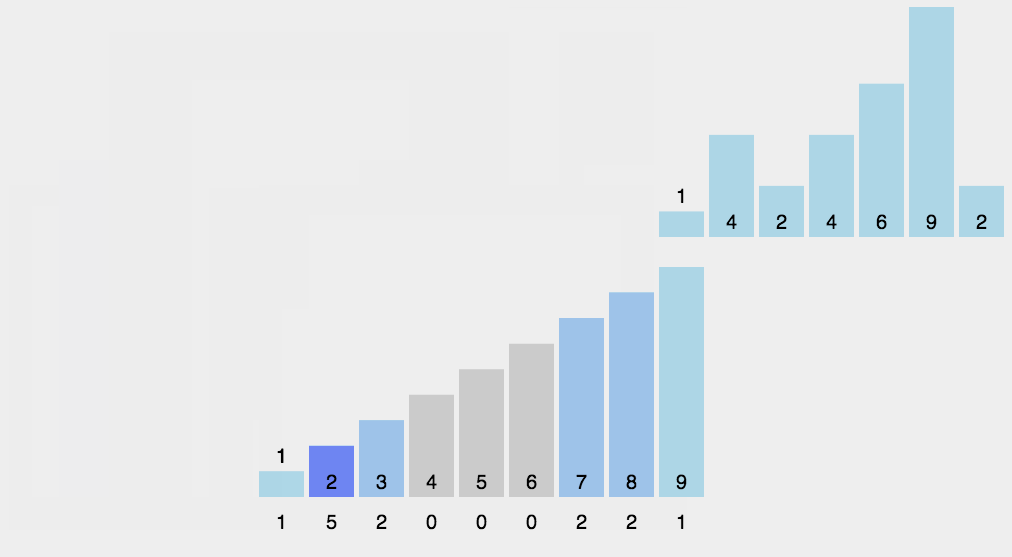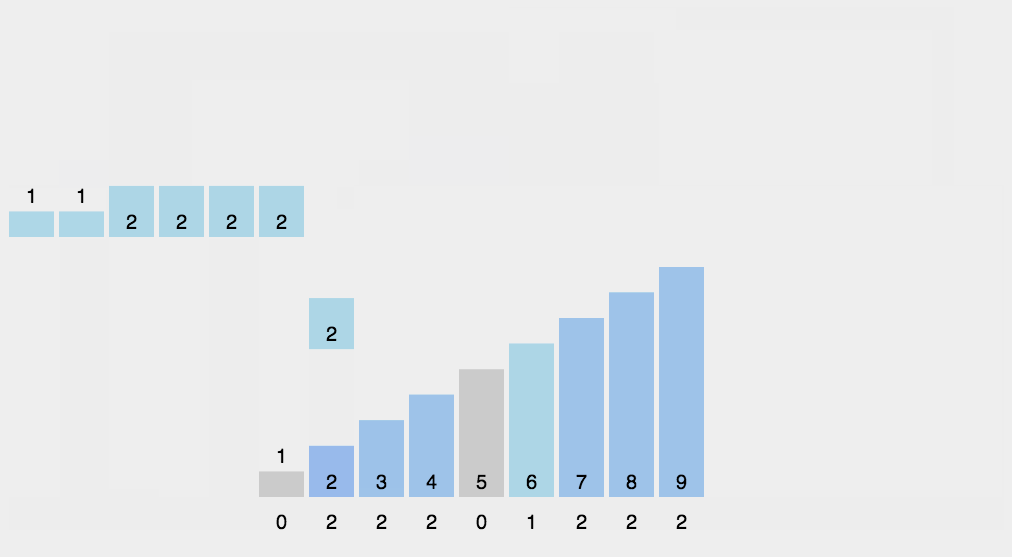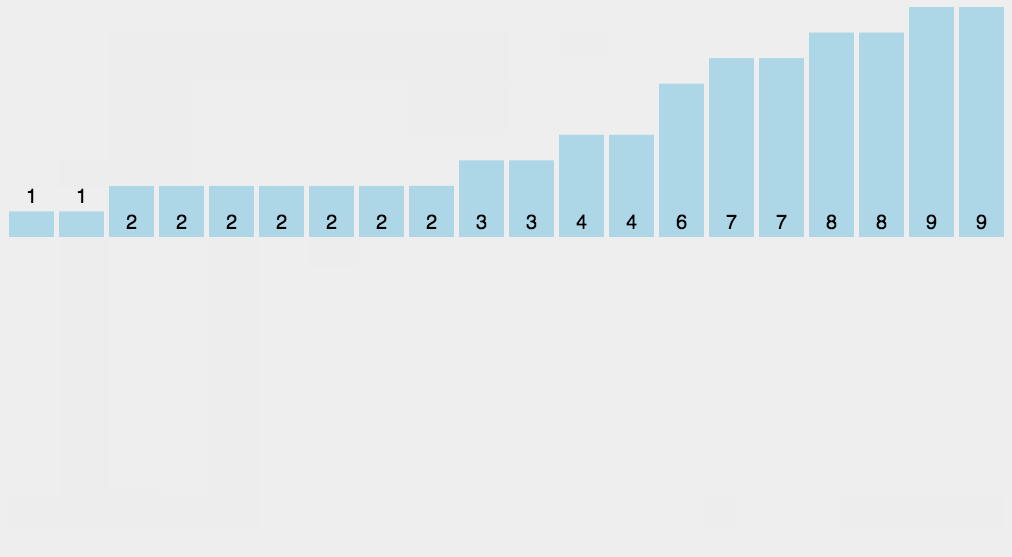
Bucket Sort

http://blogs.cuit.columbia.edu/zp2130/bucket_sort/
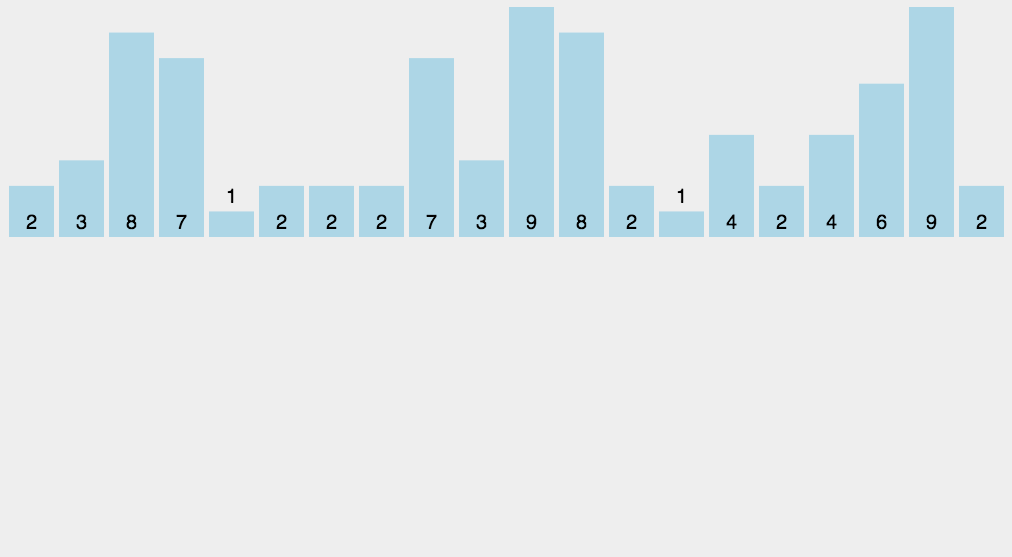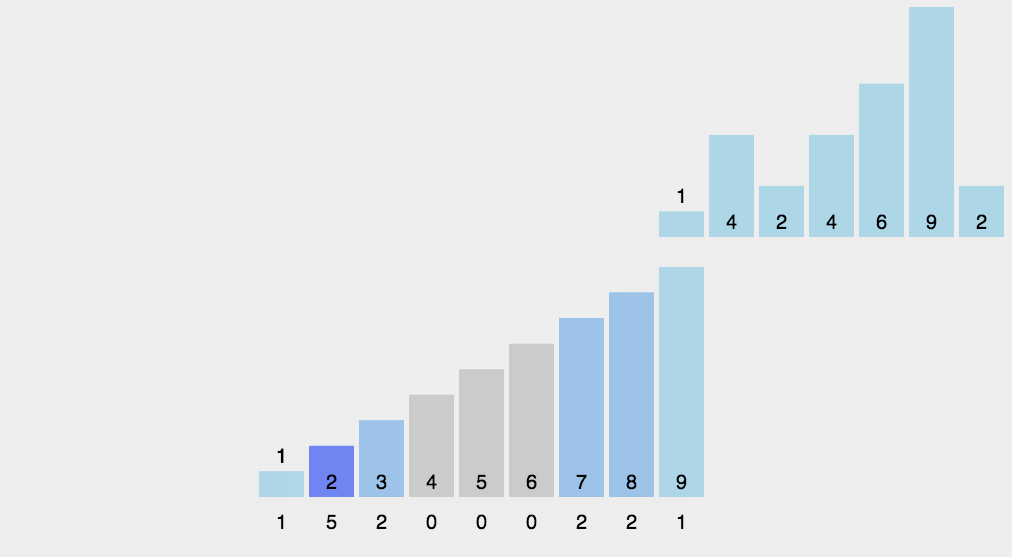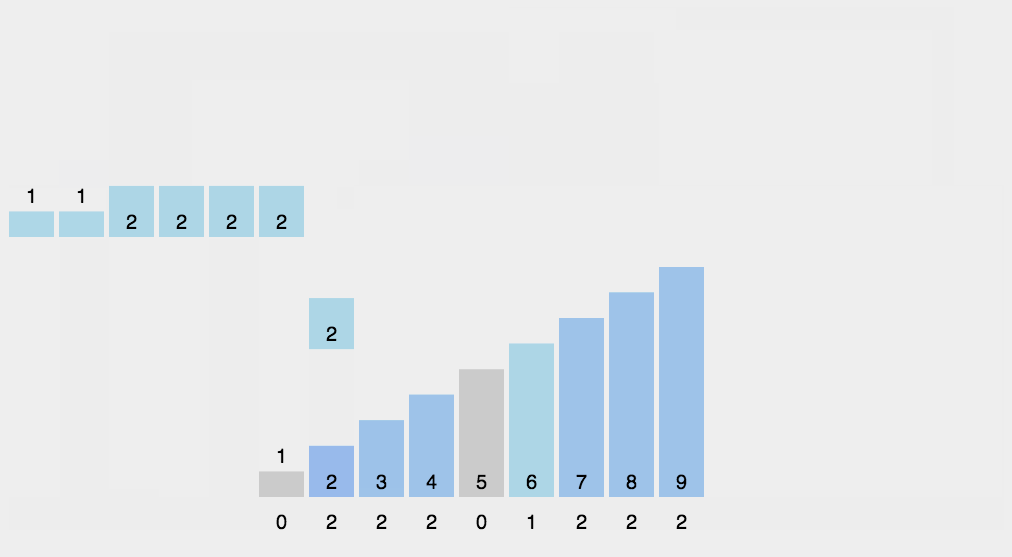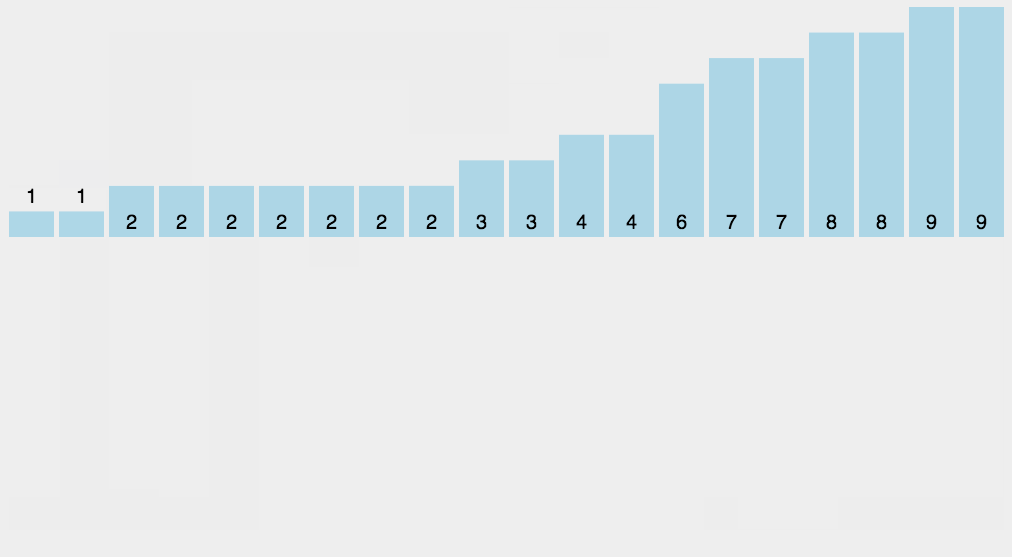
Radix Sort

http://blogs.cuit.columbia.edu/zp2130/radix_sort/

HOW TO DETERMINE COMPLEXITIES

We can determine complexity based on the type of statements used by a program. The following examples are in java but can be easily followed if you have basic programming experience and use big O notation we will explain later why big O notation is commonly used:

Constant time: O(1)

The following operations take constant time:

Assigning a value to some variable
Inserting an element in an array
Determining if a binary number is even or odd.
Retrieving element i from an array
Retrieving a value from a hash table(dictionary) with a key

They take constant time because they are “simple” statements. In this case we say the statement time is O(1)

	int example = 1;

As you can see in the graph below constant time is indifferent of input size. Declaring a variable, inserting an element in a stack, inserting an element into an unsorted linked list all these statements take constant time.

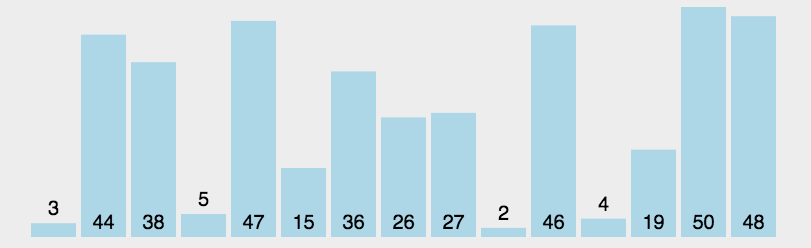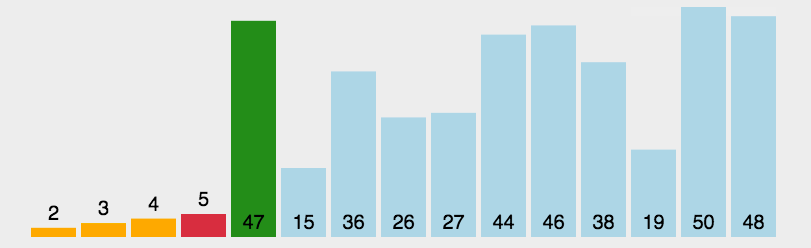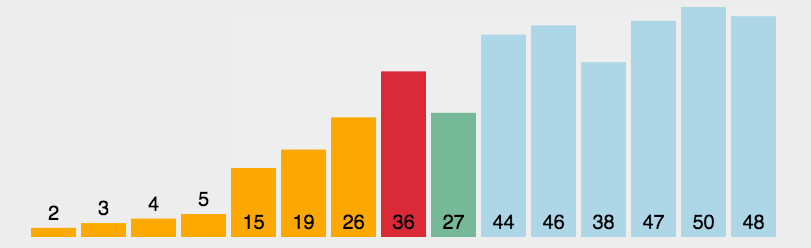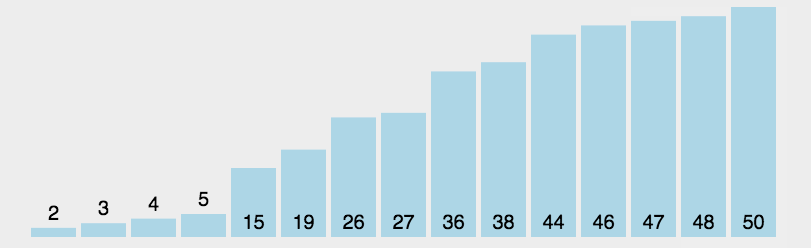
Linear time: O(n)

The next loop executes N times, if we assume the statement inside the loop is O(1), then the total time for the loop is N*O(1), which equals O(N) also known as linear time:


	for (int i = 0; i < N; i++) {
		    //do something in constant time...
	}

In the following graph we can see how running time increases linearly in relation to the number of elements n:

More examples of linear time are:

Finding an item in an unsorted collection or a unbalanced tree (worst case)
Sorting an array via bubble sort

Quadratic time: O(n²)

In this example the first loop executes N times. For each time the outer loop executes, the inner loop executes N times. Therefore, the statement in the nested loop executes a total of N * N times. Here the complexity is O(N*N) which equals O(N²). This should be avoided as this complexity grows in quadratic time


	for (int i=0; i < N; i++) {
         		for(int j=0; j< N; j++){
         			   //do something in constant time...
         		}
	}

Some extra examples of quadratic time are:

Performing linear search in a matrix
Time complexity of quicksort, which is highly improbable as we will see in the Algorithms section of this website.
Insertion sort

Algorithms that scale in quadratic time are better to be avoided. Once the input size reaches n=100,000 element it can take 10 seconds to complete. For an input size of n=1’000,000 it can take ~16 min to complete; and for an input size of n=10’000,000 it could take ~1.1 days to complete…you get the idea.

Logarithmic time: O(Log n)

Logarithmic time grows slower as N grows. An easy way to check if a loop is log n is to see if the counting variable (in this case: i) doubles instead of incrementing by 1. In the following example int i doesn’t increase by 1 (i++), it doubles with each run thus traversing the loop in log(n) time:


	for(int i=0; i < n; i *= 2) {
       	  	//do something in constant time...
    	}

Some common examples of logarithmic time are:

Binary search
Insert or delete an element into a heap

Don’t feel intimidated by logarithms. Just remember that logarithms are the inverse operation of exponentiating something. Logarithms appear when things are constantly halved or doubled.

Logarithmic algorithms have excellent performance in large data sets:

Linearithmic time: O(n*Log n)

Linearithmic algorithms are capable of good performance with very large data sets. Some examples of linearithmic algorithms are:

heapsort
merge sort
Quick sort

We’ll see a custom implementation of Merge and Quicksort in the algorithms section. But for now the following example helps us illustrate our point:


	for(int i= 0; i< n; i++) { // linear loop  O(n) * ...
          		for(int j= 1; j< n; j *= 2){ // ...log (n)
              		  //do something in constant time...
          		}
	}

Conclusion

As you might have noticed, Big O notation describes the worst case possible. When you loop through an array in order to find if it contains X item the worst case is that it’s at the end or that it’s not even present on the list. Making you iterate through all n items, thus O(n). The best case would be for the item we search to be at the beginning so every time we loop it takes constant time to search but this is highly uncommon and becomes more improbable as the list of items increases. In the next section we’ll look deeper into why big O focuses on worst case analysis.

A comparison of the first four complexities, might let you understand why for large data sets we should avoid quadratic time and strive towards logarithmic or linearithmic time:

BIG O NOTATION AND WORST CASE ANALYSIS

Big O notation is simply a measure of how well an algorithm scales (or its rate of growth). This way we can describe the performance or complexity of an algorithm. Big O notation focuses on the worst-case scenario.

Why focus on worst case performance? At first look it might seem counter-intuitive why not focus on best case or at least in average case performance? I like a lot the answer given in The Algorithms Design Manual by S. Skiena:

Imagine you go to a casino what will happen if you bring n dollars?

The best case, is that you walk out owning the casino, it’s possible but so improbable that you don’t even think about it.
The average case, is a little more tricky to prove as you need domain knowledge in order to identify which is the average case. For example, the average case in our example is that the typical bettor loses ~87% of the money that they bring to the casino, but people who are drunk surely loose even more, what about experienced professional players and what exactly is the average? How did they determined it? Who determined the average case? Are their metrics correct? Average case just makes the task of analyzing an algorithm even more complex.
The worst case is that you lose all your n dollars, this is easy to calculate and very likely to happen.

Now think of this in a context of a program with .search() method which takes linear time to execute:

The worst case is O(n), this is when the key is at the end or never present in the list. Which might happen.

The best case is O(1), this happens if and only if the key is at the beginning of the list. Which becomes even more unlikely as n grows.

DATA STRUCTURES

Data structures are fundamental constructs around which you build your application. A data structure determines the way data is stored, and organized in your computer. Whenever data exists it must have some kind of data structure in order to be stored in a computer.

Contiguous or linked data structures

Data structures can be classified as either contiguous or linked, depending whether they are based on arrays or pointers(references):

Contiguous-allocated structures, are made of single slabs of memory, some of these data structures are arrays, matrices, heaps, and hash tables.

Linked data structures, are composed as distinct chunks of memory linked together by pointers (references). Some of this data structures are lists, trees, and graph adjacency lists.

Comparison

Some advantages of linked lists over static arrays are:

Overflow is more difficult to occur on a linked structures than it is in an array. It only happens when the memory is actually full.
Insertions and deletions are simpler than for contiguous data structures such as arrays.
Linked list don’t need to know size on initialization

Advantages of arrays:

Linked structures require allocating extra space for storing pointers.
Arrays allow efficient access to any item.

ARRAY

Arrays are the fundamental contiguously allocated data structure. They have a fixed size and each element can be efficiently located by its index. Imagine an array is like a street full of houses, one right next to each other, each house can be easily located by its address (index).

The following is an example of usage of Java’s implementation of ArrayList, which is an Array that is resized when needed


               
    /*
    * We can determine at the moment of instantiation the capacity
    * of the	ArrayList this gives a little boost in performance, 
    * instead of making the array resize constantly
    */
      List<String> exampleList = new ArrayList<>(100);
       
    /*
     * Don't confuse capacity with size, the following 
     * statement outputs 0, as currently the ArrayList 
     * size is 0, but it's capacity is 100
     */
      System.out.println(exampleList.size());
   
      exampleList.add("first");
      exampleList.add("second");
      exampleList.add("third");
      
      System.out.println(exampleList.size());//prints 3

SET

A Set is a Collection that cannot contain duplicate elements.

In Java the Set interface contains methods inherited from Collection and adds the restriction that duplicate elements are prohibited. Java also adds a stronger contract on the behavior of the equals() and hashCode() methods, allowing Set instances to be compared meaningfully even if their implementation types differ. Some methods declared by Set are:

add( ) Adds an object to the collection
clear( ) Removes all objects from the collection
contains( ) Returns true if a specified object is an element within the collection
isEmpty( ) Returns true if the collection has no elements
iterator( ) Returns an Iterator object for the collection which may be used to retrieve an object
remove( ) Removes a specified object from the collection
size( ) Returns the number of elements in the collection

Let’s use an example of Java’s implementation of set to understand how it works. First, we need to define the DataType and override the equals() and hashCode() methods:


   public class DataType {
   	private String name;
   	private int number;
   	
   	public DataType(String name, int number){
   		this.name = name;
   		this.number = number;
   	}
   
   	@Override
   	public int hashCode() {
   		final int prime = 31;
   		int result = 1;
   		result = prime * result + ((name == null) ? 0 :
   		 name.hashCode());
   		return result;
   	}
   
   	    
      /*
      * We override method equals so that objects 
      * with same name can't be added to the set, 
      * but objects with same numbers can be added
      */
   	@Override
   	public boolean equals(Object obj) {
   		if (obj == null)
   			return false;
   		
   		if (this.getClass() != obj.getClass())
   			return false;
   		
   		DataType other = (DataType) obj;
   		if (other.name == null) 
   				return false;
   				
   		return this.name.equals(other.name);
   	}
   
   	@Override
   	public String toString() {
   		return "DataType: name=" + name + ", number=" + number;
   	}
   }

Now we can proceed to use the class


   Set<DataType> example = new HashSet<>();
   	
   DataType data1 = new DataType("first", 1);
       	
   //notice name repeated it's not valid
   DataType data2 = new DataType("first", 1);
       
   //notice different name but same number it's valid
   DataType data3 = new DataType("second", 1);
   	
   example.add(data1);
   example.add(data2);
   example.add(data3);
   
   for (DataType x : example){
   	System.out.println(x);
   }

the output is:


   DataType: name=first, number=1
   DataType: name=second, number=1

Multiset

A multiset is similar to a set but allows repeated values. For Java, third-party libraries provide multiset functionality

Apache Commons Collections provides the Bag and SortedBag interfaces, with implementing classes like HashBag and TreeBag.
Google Guava provides the Multiset interface, with implementing classes like HashMultiset and TreeMultiset.

This data structure is perfect for when we need to perform statistical data that needs no sorting, for example calculating the average or Standard Deviation of a multiset.

STACKS AND QUEUES

Arrays, Linked list, Trees are best use to represent real objects, Stacks & Queues are best to complete tasks, they are like a tool to complete and then discard.

They are useful to manage data in more a particular way than arrays and lists.

Queue are first in, first out (FIFO)
Stack are last in, first out (LIFO)

When to use stacks and queues:

Use a queue when you want to get things out in the order that you put them in.
Use a stack when you want to get things out in the reverse order than you put them in.
Use a list when you want to get anything out, regardless of when you put them in (and when you don’t want them to automatically be removed).

The following is an implementation of Queues in Java, based on the course by R.Sedgewick in coursera


       
   /*This implementation uses a singly-linked list 
    * with a static nested class for linked-list nodes. 
    * All operations take constant O(1) time in the worst case.
    */
   public class Queue<Generic> implements Iterable<Generic> {
      	private Node<Generic> firstNode; // beginning of queue
      	private Node<Generic> lastNode; // end of queue
      	private int size; // number of elements on queue
      
      	private static class Node<Item> {
      		private Item item;
      		private Node<Item> next;
      	}
      
      	public Queue() {
      		firstNode = null;
      		lastNode = null;
      		size = 0;
      	}
      
      	public boolean isEmpty() {
      		return firstNode == null;
      	}
      
      	public int size() {
      		return size;
      	}
      
      	public Generic peek() {
      		if (isEmpty())
      			throw new NoSuchElementException("Queue underflow");
      		return firstNode.item;
      	}
      
      	public void enqueue(Generic item) {
      		Node<Generic> oldlast = lastNode;
      		lastNode = new Node<Generic>();
      		lastNode.item = item;
      		lastNode.next = null;
      		if (isEmpty())
      			firstNode = lastNode;
      		else
      			oldlast.next = lastNode;
      		size++;
      	}
      
      	public Generic dequeue() {
      		if (isEmpty())
      			throw new NoSuchElementException("Queue underflow");
      		Generic item = firstNode.item;
      		firstNode = firstNode.next;
      
      		if (isEmpty())
      			lastNode = null;// to avoid loitering
      		size--;
      		return item;
      	}
      
      	public String toString() {
      		StringBuilder s = new StringBuilder();
      		for (Generic item : this)
      			s.append(item + " ");
      		return s.toString();
      	}
      
      	public Iterator<Generic> iterator() {
      		return new ListIterator<Generic>(firstNode);
      	}
      
      	private class ListIterator<Item> implements Iterator <Item> {
      		private Node <Item> current;
      
      		public ListIterator(Node<Item> first) {
      			current = first;
      		}
      
      		public boolean hasNext() {
      			return current != null;
      		}
      
      		public void remove() {
      			throw new UnsupportedOperationException();
      		}
      
      		public Item next() {
      			if (!hasNext())
      				throw new NoSuchElementException();
      			Item item = current.item;
      			current = current.next;
      			return item;
      		}
      	}
      
      	public static void main(String[] args) {
      		Queue<String> q = new Queue<>();
      		q.enqueue("FIRST IN");
      		q.enqueue(" 2nd ");
      		q.enqueue(" 3rd ");
      
      		System.out.println(q.dequeue() + " first out ==> FIFO");
      	}
   }

DICTIONARIES

A Dictionary is a data structure that maps a key to a value.This is useful in cases where you want to be able to access data via a particular key rather than an integer index.

In Java, Dictionaries are implemented as a Map: The Map interface maps unique keys to values. A key is an object that you use to retrieve a value at a later date.

Given a key and a value, you can store the value in a Map object. After the value is stored, you can retrieve it by using its key.

Following is a simple Map Implementation as an array. Firstly, we create a class to help store the key and it’s value in an object:


   public class Entry<K, V> {
      private final K key;
      private V value;
      
      public Entry(K key, V value) {
      	this.key = key;
      	this.value = value;
      }
      
      public K getKey() {
      	return key;
      }
      
      public V getValue() {
      	return value;
      }
      
      public void setValue(V value) {
      	this.value = value;
      }
   }

Then the implementation of map:


   public class Map<K, V> {
      private int size;
      private int CAPACITY = 16;
      private Entry<K, V>[] entriesArray = new Entry[CAPACITY];
      
      public void put(K key, V value) {
      	boolean insert = true;
      	for (int i = 0; i < size; i++) {
      		if (entriesArray[i].getKey().equals(key)) {
      			entriesArray[i].setValue(value);
      			insert = false;
      		}
      	}
      	if (insert) {
      		growArray();
      		entriesArray[size++] = new Entry<K, V>(key, value);
      	}
      }
      
      private void growArray() {
      	if (size == entriesArray.length) {
      		int newSize = entriesArray.length * 2;
      		entriesArray = Arrays.copyOf(entriesArray, newSize);
      	}
      }
      
      public V get(K key) {
      	for (int i = 0; i < size; i++) {
      		if (entriesArray[i] != null) {
      			if (entriesArray[i].getKey().equals(key)) {
      				return entriesArray[i].getValue();
      			}
      		}
      	}
      	return null;
      }
      
      public void remove(K key) {
      	for (int i = 0; i < size; i++) {
      		if (entriesArray[i].getKey().equals(key)) {
      			entriesArray[i] = null;
      			size--;
      			condenseArrayElements(i);
      		}
      	}
      }
          
       //Moves backwards elements from start arg
       private void condenseArrayElements(int start){ 
        for (int i = start; i < size; i++) {
      	  entriesArray[i] = entriesArray[i+1];
        }
       }
       
       public int size(){ return size; }
      
        public Set<K> keySet(){
        Set<K> set = new HashSet<K>();
        for (int i = 0; i < size; i++) {
         set.add(entriesArray[i].getKey());
        }
        return set;
       }
      
        public static void main(String[] args) {
      	  Map<String, Integer> mapExample = new Map<>();
      	   mapExample.put("Key 1", 100);
      	  System.out.println(mapExample.get("Key 1"));
      	  
      	  mapExample.put("Key 2", 200);
      	  mapExample.put("Woaah", 100000);
      	  System.out.println(mapExample.get("Key 2"));
      	    
      	  System.out.println("keySet: " + mapExample.keySet());
      	 
      	  System.out.print("Values: ");
      	  for (String key : mapExample.keySet()){
      	   System.out.print(mapExample.get(key) + " ");
      	  }
      	    mapExample.remove("Key 2");
      	  System.out.println("\nkeySet: " + mapExample.keySet());
      	 }
   }

SEARCHING AND SORTING

In this section we are going to review searching and sorting algorithms.

Why is sorting so important

The first step in organizing data is sorting. Lots of tasks become easier once a data set of items is sorted
Some algorithms like binary search are built around a sorted data structure.
In accordance to S. Skiena computers have historically spent more time sorting than doing anything else. Sorting remains the most ubiquitous combinatorial algorithm problem in practice.

Considerations:

How to sort: descending order or ascending order?
Sorting based on what? An object name (alphabetically), by some number defined by its fields/instance variables. Or maybe compare dates, birthdays, etc.
What happens with equals keys, for example various people with the same name: John, then sort them by Last Name.
Does your sorting algorithm sorts in place or needs extra memory to hold another copy of the array to be sorted. This is even more important in embedded systems.

Java uses Comparable interface for sorting and returns: +1 if compared object is greater, -1 if compared object is less and 0 if compared objects are equal.

Sorting becomes more ubiquitous when we think on all the things we do daily that are previously sorted for us to understand and have better access to them:

Imagine trying to find a phone number in an unsorted phone book, or searching for a word in an unsorted dictionary.
Your MP3 player can sort your lists by artists name, genre, song name, ratings.
Search engines display results in descending order of importance
Spreadsheets can be sorted in various ways to work better with their contents

Searching

There are two types of searching algorithms: Those that need a previously ordered data structure in order to work properly, and those that don’t need an ordered list.

Searching is also very important for many computing applications: searching through a search engine, finding a bank account balance for some client, searching in a large data set for a particular value, searching in your directories for some needed file. Many applications rely on effective search, if your application is complete but takes long too perform a search and retrieve data it will be discarded as useless.

SELECTION SORT

It is called selection sort because it repeatedly selects the smallest remaining item:

Find the smallest element. Swap it with the first element.
Find the second smallest element. Swap it with the second element
Find the third smallest element. Swap it with the third element
Repeat finding the smallest element and swapping in the correct position until the list is sorted

Implementation in java for selection sort:


    public class SelectionSort {
    
       public static void selectionSort(Comparable[] array) {
      
        for (int i = 0; i < array.length; i++) {
         int min = i;
         for (int j = i + 1; j < array.length; j++) {
          if (isLess(array[j], array[min])) {
           min = j;
          }
         }
         swap(array, i, min);
        }
       }
       
       //returns true if Comparable j is less than min
       private static boolean isLess(Comparable j, Comparable min) {
        int comparison = j.compareTo(min);
        return  comparison< 0;
       }
      
       private static void swap(Comparable[] array, int i, int j) {
        Comparable temp = array[i];
        array[i] = array[j];
        array[j] = temp;
       }
      
       public static <E> void printArray(E[] array) {
        for (int i = 0; i < array.length; i++) {
         System.out.print(array[i] + " ");
        }
       }
       
       // Check if array is sorted
       public static boolean isSorted(Comparable[] array) {
        for (int i = 1; i < array.length; i++) {
         if (isLess(array[i], array[i - 1])) {
          return false;
         }
        }
        return true;
       }
       
        public static void main(String[] args) {
      	  Integer[] intArray = { 34, 17, 23, 35, 45, 9, 1 };
      	  System.out.println("Unsorted Array: ");
      	  printArray(intArray);
      	  System.out.println("\nIs intArray sorted? "
            + isSorted(intArray));
      	
      	  selectionSort(intArray);
      	  System.out.println("\nSelection sort:");
      	  printArray(intArray);
      	  System.out.println("\nIs intArray sorted? "
            + isSorted(intArray));
      	
      	  String[] stringArray = { "z", "g", "c", "o", "a",
            "@", "b", "A", "0", "." };
      	  System.out.println("\n\nUnsorted Array: ");
      	  printArray(stringArray);
      	
      	  System.out.println("\n\nSelection sort:");
      	  selectionSort(stringArray);
      	  printArray(stringArray);
       }
   }

Output is:

         
   Unsorted Array: 
   34 17 23 35 45 9 1 
   Is intArray sorted? false
   
   Selection sort:
   1 9 17 23 34 35 45 
   Is intArray sorted? true
   
   
   Unsorted Array: 
   z g c o a @ b A 0 . 
   
   Selection sort:
   . 0 @ A a b c g o z

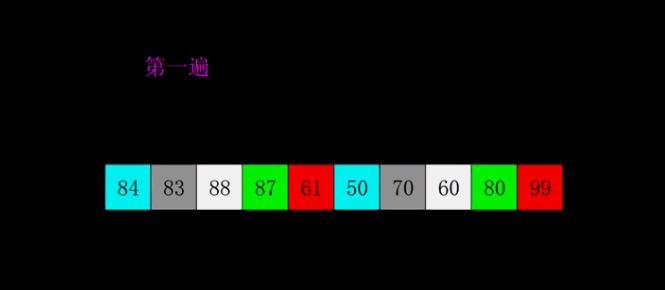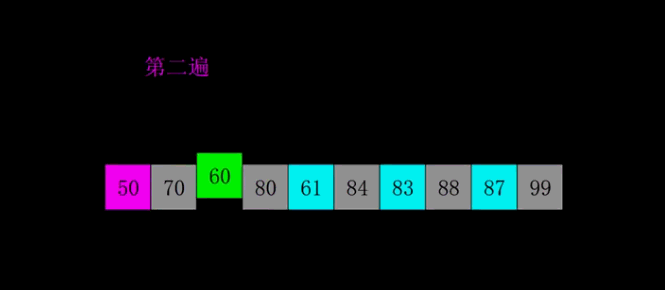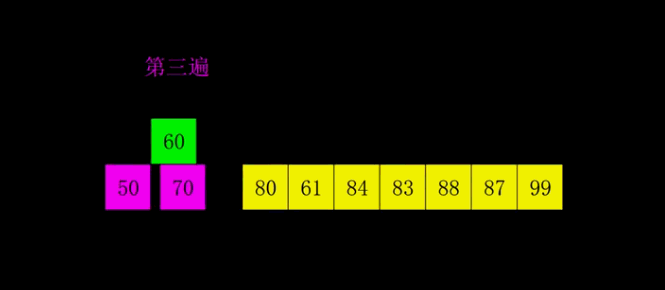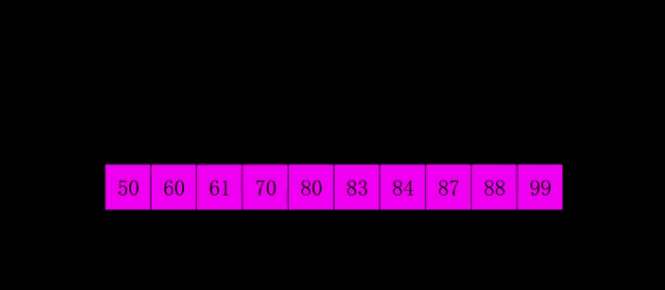
SHELLSORT

Shell sort is perfect good for embedded systems as it doesn’t require a lot of extra memory allocation; it is also useful for small to medium size arrays. Lets see the following implementation in java code:


   public class ShellSort {
   
    public static void shellSort(Comparable[] array) {
     int N = array.length;
     int h = 1;
     while (h < N/3) h = 3*h + 1;
     while (h >= 1){
      for (int i=h; i<N ; i++) {
       for(int j=i; j>=h && isLess(array[j], array[j-h]); j-=h){
        swap(array, j, j-h);
       }
      }
      h = h/3;
     }
    }
   
    // returns true if Comparable j is less than min
    private static boolean isLess(Comparable j, Comparable min) {
    
     int comparison = j.compareTo(min);
     return comparison< 0;
     
    }
   
    private static void swap(Comparable[] array, int i, int j) {
    
     Comparable temp = array[i];
     array[i] = array[j];
     array[j] = temp;
     
    }
   
    public static <E> void printArray(E[] array) {
    
     for (int i = 0; i < array.length; i++) {
      System.out.print(array[i] + " ");
     }
     
    }
   
    // Check if array is sorted
    public static boolean isSorted(Comparable[] array) {
    
     for (int i = 1; i < array.length; i++) {
      if (isLess(array[i], array[i - 1])) {
       return false;
      }
     }
     return true;
    }
   
    public static void main(String[] args) {
    
     Integer[] intArray = { 34, 1000, 23, 2, 35, 0, 9, 1 };
     System.out.println("Unsorted Array: ");
     printArray(intArray);
     System.out.println("\nIs intArray sorted? " + isSorted(intArray));
   
     shellSort(intArray);
     System.out.println("\nSelection sort:");
     printArray(intArray);
     System.out.println("\nIs intArray sorted? " + isSorted(intArray));
   
     String[] stringArray = { "z", "Z","999", "g", "c", "o",
         "a", "@", "b", "A","0", "." };
     System.out.println("\n\nUnsorted Array: ");
     printArray(stringArray);
   
     System.out.println("\n\nSelection sort:");
     shellSort(stringArray);
     printArray(stringArray);
    }
   }

Output:


   Unsorted Array: 
   34 1000 23 2 35 0 9 1 
   Is intArray sorted? false
   
   Selection sort:
   0 1 2 9 23 34 35 1000 
   Is intArray sorted? true
   
   
   Unsorted Array: 
   z Z 999 g c o a @ b A 0 . 
   
   Selection sort:
   . 0 999 @ A Z a b c g o z

MERGESORT

Mergesort is also called divide and conquer algorithm, because it divides the original data into smaller pieces of data to solve the problem. Merge sort works in the following way:

Divide into 2 collections. Mergesort will take the middle index in the collection and split it into the left and right parts based on this middle index.
Resulting collections are again recursively splited and sorted
Once the sorting of the two collections is finished, the results are merged
Now Mergesort it picks the item which is smaller and inserts this item into the new collection.
Then selects the next elements and sorts the smaller element from both collections


   public class MergeSort {
   
       public int[] sort(int [] array){
        mergeSort(array, 0, array.length-1);
        return array;
        
       }
       
       private void mergeSort(int[] array, int first, int last) {
       
        // We need mid to divide problem into smaller size pieces
        int mid = (first + last) / 2;
        
        //If first < last the array must be recursively sorted
        if (first < last) {
         mergeSort(array, first, mid);
         mergeSort(array, mid + 1, last);
        }
        
        //merge solved pieces to get solution to original problem
        int a = 0, f = first, l = mid + 1;
        int[] temp = new int[last - first + 1];
      
        while (f <= mid && l <= last) {
         temp[a++] = array[f] < array[l] ? array[f++] : array[l++];
        }
        
        while (f <= mid) {
         temp[a++] = array[f++];
        }
        
        while (l <= last) {
         temp[a++] = array[l++];
        }
        
        a = 0;
        while (first <= last) {
         array[first++] = temp[a++];
        }
       }
       
       public static void printArray(int[] array) {
        for (int i = 0; i < array.length; i++) {
         System.out.print(array[i] + " ");
        }
        
       }
      
       public static void main(String[] args) {
       
        System.out.println("Original array:");
        int[] example = { 100, 30, 55, 62, 2, 42, 20, 9, 394, 1, 0 };
        printArray(example);
        
        System.out.println("\nMergesort");
        MergeSort merge = new MergeSort();
        merge.sort(example);
        printArray(example);
        
       }
   }

Output:


   Original array:
   100 30 55 62 2 42 20 9 394 1 0 
   Mergesort
   0 1 2 9 20 30 42 55 62 100 394

QUICKSORT

Quick sort is better than merge sort from a memory usage comparison. Because quick sort doesn’t require additional storage to work. It only uses a small auxiliary stack.

Skiena discovered via experimentation that a properly implemented quicksort is typically 2-3 times faster than mergesort or heapsort

The pseudo-code for quicksort is:

If the array contains only 1 element or 0 elements then the array is sorted.
If the array contains more than 1 element:
Select randomly an element from the array. This is the “pivot element”.
Split into 2 arrays based on pivot element: smaller elements than pivot go to the first array, the ones above the pivot go into the second array
Sort both arrays by recursively applying the Quicksort algorithm.
Merge the arrays

Quicksort may take quadratic time O(n²) to complete but this is highly improbable to occur. This happens when the partitions are unbalanced. For example, the first partition is on the smallest item, the second partition of the next smallest item, so each time the program just remove one item for each call, leading to a large number of partitions of large sub arrays .If the collection of elements is previously randomized the most probable performance time for quicksort is Θ (n log n). So if you’re having problems with performance of quicksort, you can rearrange randomly elements in the collection this will increase the probability of quicksort to perform in Θ (n log n).

Implementation of quicksort:


   import java.util.Random;
   
   public class QuickSort {
   
       public void quicksort(int[] array) {
        quicksort(array, 0, array.length - 1);
       }
       
       private void quicksort(int[] array, int first, int last) {
        if (first < last) {
         int pivot = partition(array, first, last);
         
         // Recursive call
         quicksort(array, first, pivot - 1);
         quicksort(array, pivot + 1, last);
        }
       }
       
       private int partition(int[] input, int first, int last) {
       
        /*
        *notice how pivot is randomly selected this makes O(n^2) 
        *very low probability
        */
        int pivot = first + new Random().nextInt(last - first + 1); 
        
        swap(input, pivot, last);
        for (int i = first; i < last; i++) {
         if (input[i] <= input[last]) {
          swap(input, i, first);
          first++;
         }
        }
        
        swap(input, first, last);
        return first;
       }
       
       private void swap(int[] input, int a, int b) {
        int temp = input[a];
        input[a] = input[b];
        input[b] = temp;
       }
       
       public static void printArray(int[] array) {
        for (int i = 0; i < array.length; i++) {
         System.out.print(array[i] + " ");
        }
       }
       
       public static void main(String[] args) {
       
        int[] example = { 90, 6456, 20, 34, 65, -1, 54, -15, 
        1, -999, 55, 529, 0 }; 
        System.out.println("Original Array");
        printArray(example);
        System.out.println("\n\nQuickSort");
        QuickSort sort = new QuickSort();
        sort.quicksort(example);
        printArray(example);
        
       }
   }

Output:


   Original Array
   90 6456 20 34 65 -1 54 -15 1 -999 55 529 0 
   
   QuickSort
   -999 -15 -1 0 1 20 34 54 55 65 90 529 6456

LINEAR SEARCH

This is the most basic type of search, easy to implement and understand but inefficient for extremely large data sets. Let’s look at the following implementation:


   public class LinearSearch {
   
      public static void main(String[] args) {
         int[] array = { 0, 2, 9, 10, 100, -2, -3, 
                        902, 504, -1000, 20, 9923 };
         
         System.out.println(linearSearch(array, 100)); 
         //prints: 100 found at position index: 4
         
         System.out.println(linearSearch(array, -1)); 
         //prints: not found
         
         System.out.println(linearSearch(array, 9923));
         //prints: 9923 found at position index: 11
      }
      
      private static String linearSearch(int[] array, int toSearch){
         String result ="not found";
         
         for (int i=0; i< array.length; i++){
            if(array[i]==toSearch){
               result = array[i] +" found at position index: " + i;
               break;
            }
         }
         return result;
      }
   }

BINARY SEARCH

Binary search is also easy to implement and easy to understand. We actually make use of binary search without knowing when searching in a dictionary for a specific word or in a phone book. Technically it’s not the same but it is a very similar process.

We open a dictionary more or less by the middle if the word we are searching for starts in a letter over the middle, we discard the first half of the dictionary and now focus more or less by the middle of the second half. If the word is below the middle of the second half, we discard the top half and keep applying this same technique until we find our word

Let’s look at the pseudocode to make this idea clearer:

Receive a sorted array of n elements
Compute middle point
If index toSearch is less than array[mid] then highestIndex = mid -1 (This changes mid)
If index toSearch is greater than array[mid] then lowestIndex = mid +1
else if index isn’t greater nor less than array[mid], this means it’s equal so return 0
If not greater, less nor equal, then it’s not in the array so return -1


   public class BinarySearch {
   
    private BinarySearch(){ } //Constructor
   
    public static int binarySearch(int toSearch, int[]array){
        int lowestIndex = 0;
        int highestIndex = array.length -1;
     
       while (lowestIndex <= highestIndex){
                  int mid = lowestIndex + 
                     (highestIndex - lowestIndex)/2;
   
                   if  ( toSearch < array[mid]) 
                         highestIndex = mid -1;
      
                  else if ( toSearch > array[mid]) 
                              lowestIndex = mid + 1;
      
                   else if (toSearch==array[mid])
                               return mid;
       }
       return -1;
    }
    
    public static void main(String[] args) {
     int [] array = { -100, 1 , 2, 3, 4, 5, 100, 999, 10203};
     
     System.out.println(binarySearch(999, array));  //returns index 6
     System.out.println(binarySearch(-100, array)); //returns index 0
     System.out.println(binarySearch(6, array));    //returns index -1
    }
    
   }

Java implements its own .binarySearch() static methods in the classes Arrays and Collections in the standard java.util package for performing binary searches on Java arrays and on Lists, respectively. They must be arrays of primitives, or the arrays or Lists must be of a type that implements the Comparable interface, or you must specify a custom Comparator object.

Email Address:

Blog Stats

State Action/Control

Meta

WHAT IS AN ALGORITHM?

ALGORITHM EFFICIENCY

Bubble Sort

Selection Sort

Insertion Sort

Shell Sort

Merge Sort

Quick Sort

Heap Sort

Counting Sort

Bucket Sort

HOW TO DETERMINE COMPLEXITIES

Constant time: O(1)

Linear time: O(n)

Quadratic time: O(n2)

Logarithmic time: O(Log n)

Linearithmic time: O(n*Log n)

Conclusion

BIG O NOTATION AND WORST CASE ANALYSIS

DATA STRUCTURES

Contiguous or linked data structures

Comparison

ARRAY

SET

Multiset

STACKS AND QUEUES

DICTIONARIES

SEARCHING AND SORTING

Why is sorting so important

Considerations:

Searching

SELECTION SORT

SHELLSORT

MERGESORT

QUICKSORT

LINEAR SEARCH

BINARY SEARCH

Comments

Leave a Reply Cancel reply

Last posts

Quadratic time: O(n²)