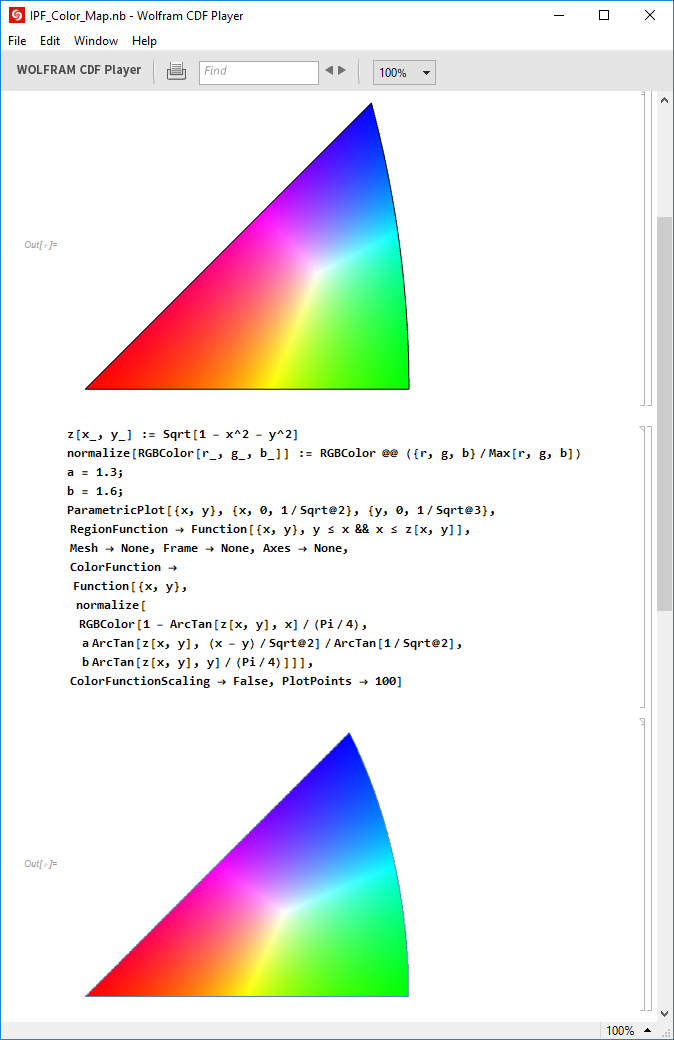
Euler Angles Bunge vs Elastic
Euler Angles Bunge
MATLAB code @github private repository
Euler Angles Elastic
MATLAB code @github private repository
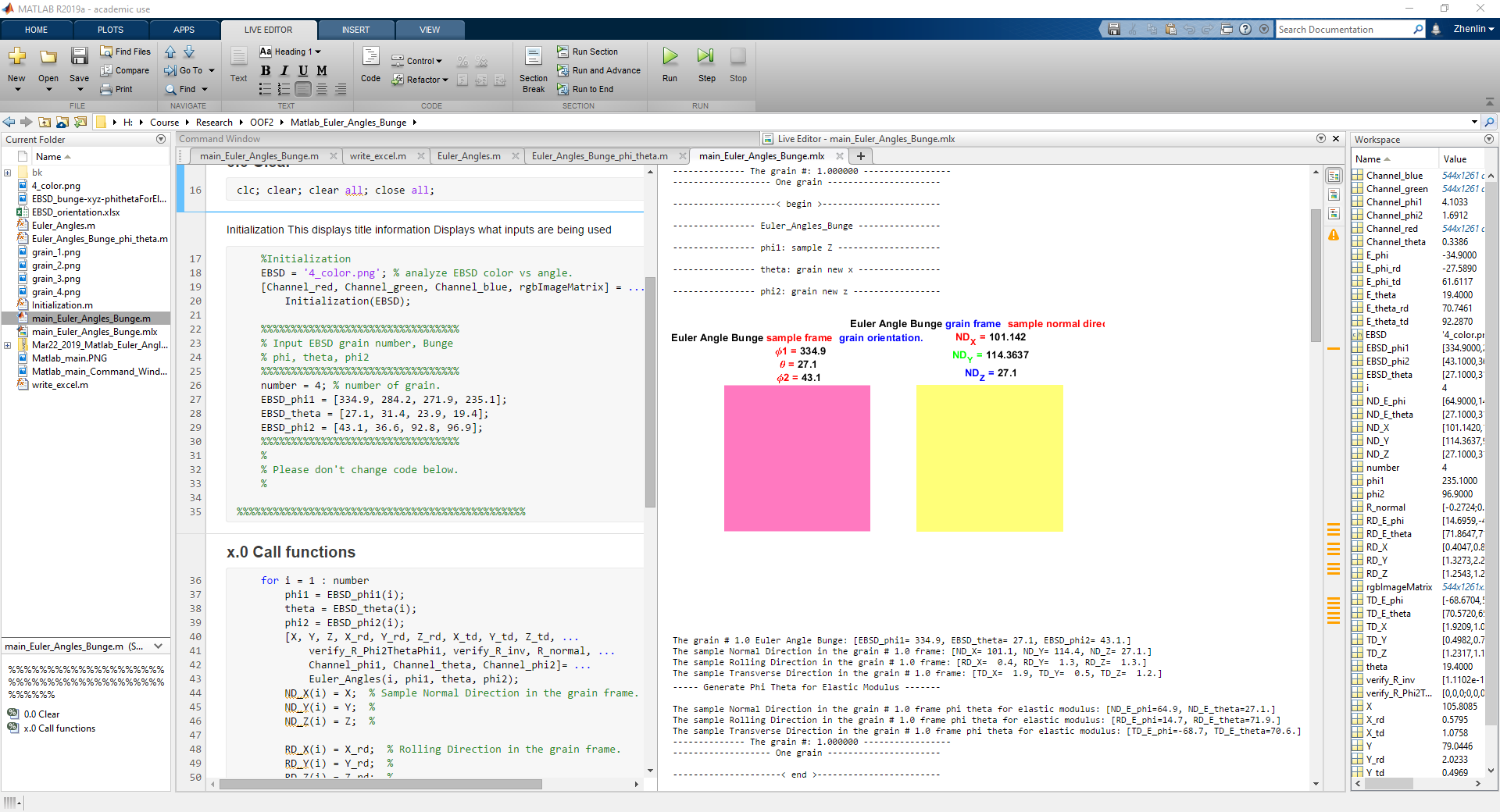
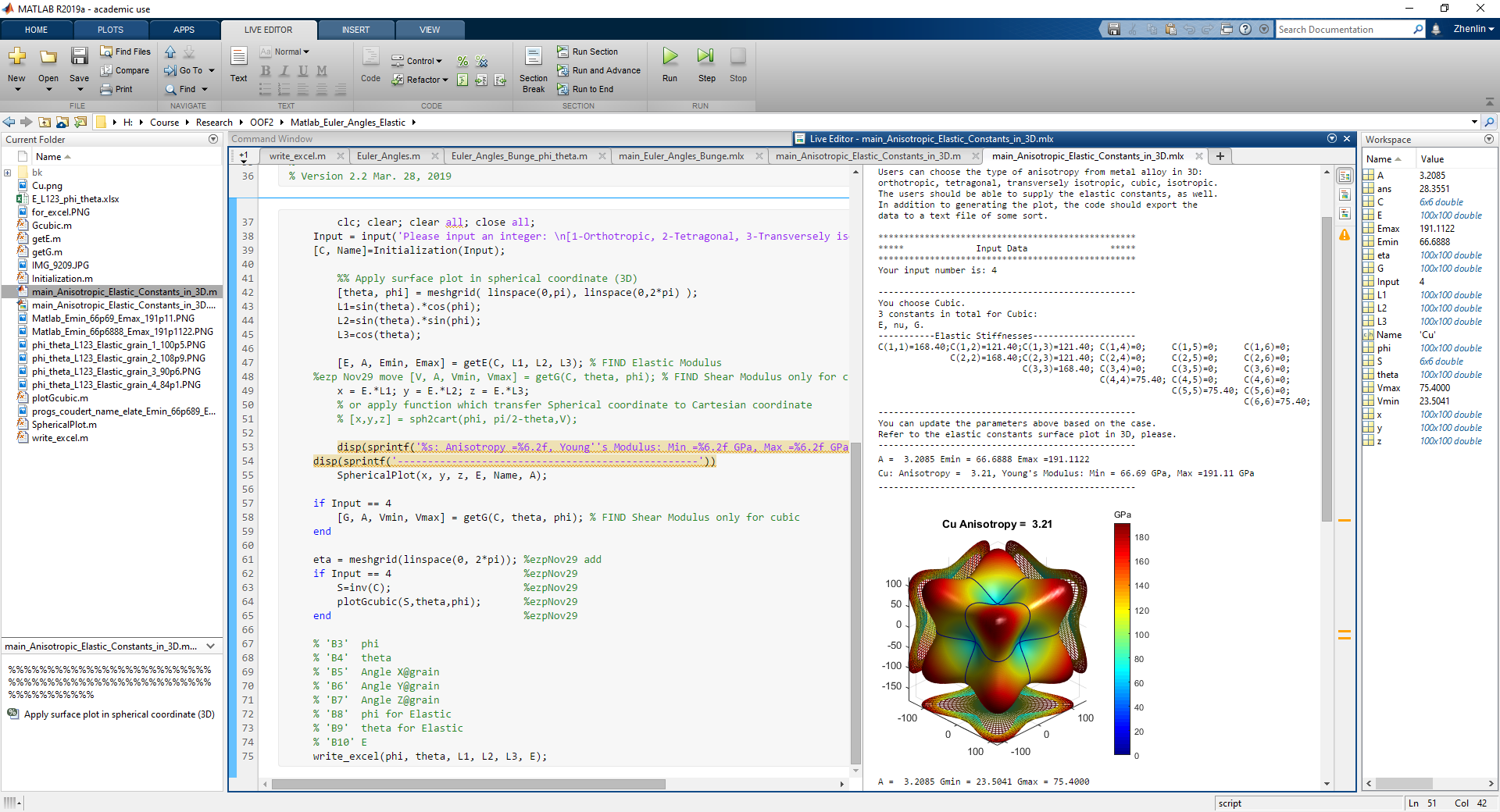
MATLAB code @github private repository
The MATLAB code outputs the sample Normal direction (Rolling direction, Transverse direction) in the grain frame. ‘main_Euler_Angles_Bunge.m’ works as ‘API’ in which you can input EBSD grain number, Bunge. The functions are defined in other m files. Finally, it outputs Normal direction (Rolling direction, Transverse direction) in the grain frame and phi & theta for elastic modulus in one excel file.
MATLAB code @github private repository
The MATLAB code outputs the sample normal direction in the grain frame. ‘main_Euler_Angles_Elastic.m’ works as ‘API’. The functions are defined in other m files. Finally, it outputs normal direction in the grain frame and phi & theta vs elastic modulus in one excel file.
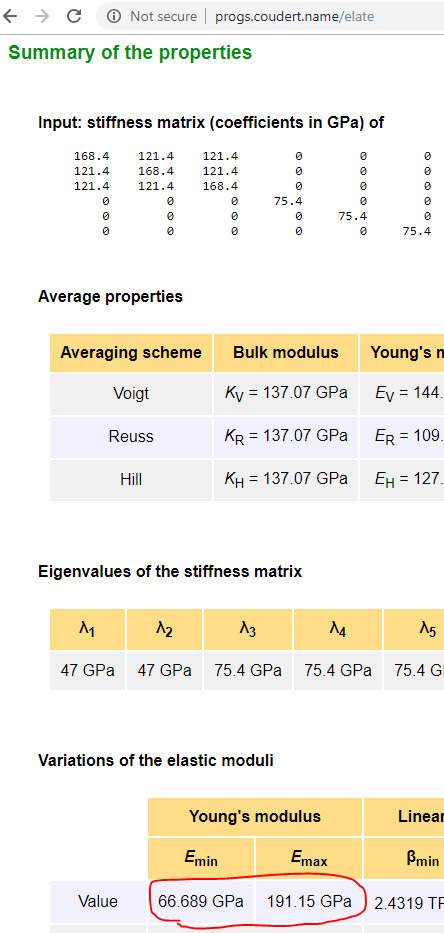
Verify progs.coudert.name/elate
EBSD Euler Angles Bunge (phi1, theta, phi2) -> XYZ -> phi, theta for Elastic
theta in Bunge is different from theta for Elastic, please refer to the description at 2 sections: Euler Angle Bunge and Normal direction in the Grain frame
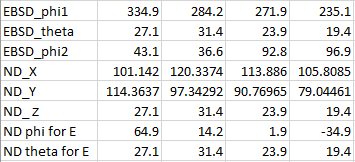
phi,theta for MATLAB plotting Orientation vs Elastic -> Angle wrt xyz@grain frame -> phi,theta for Searching Elastic -> Elastic
Grain 1-4

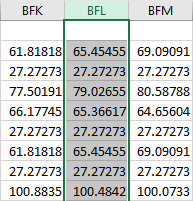
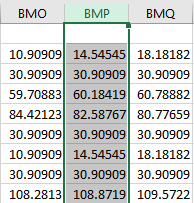
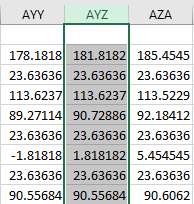
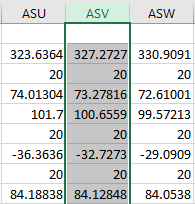
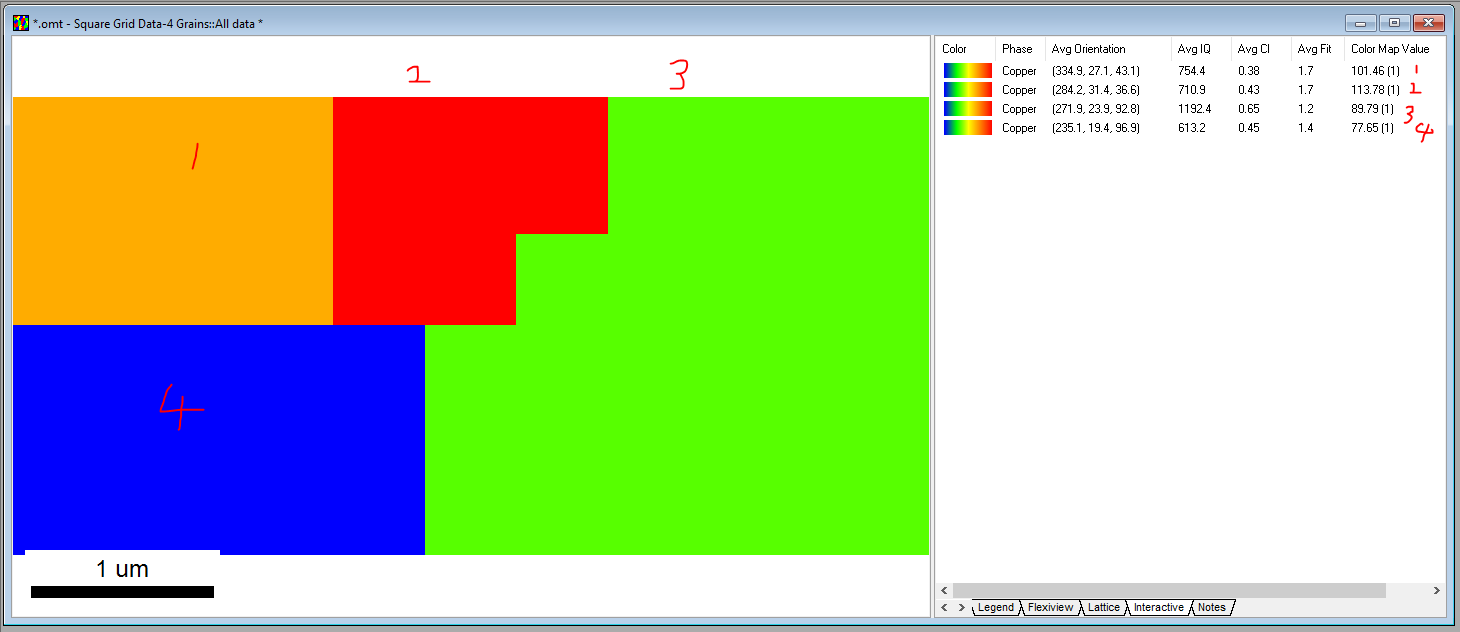
Euler Angle Bunge
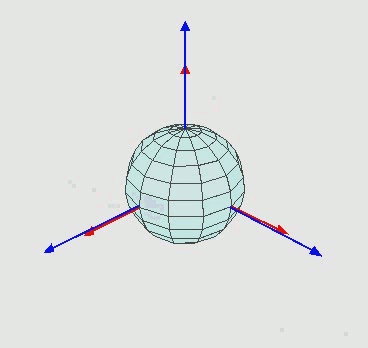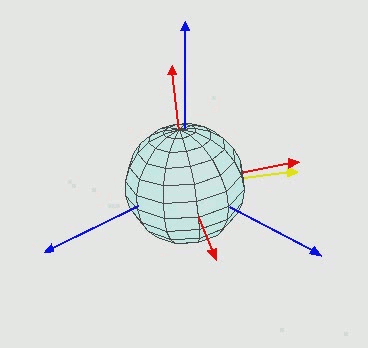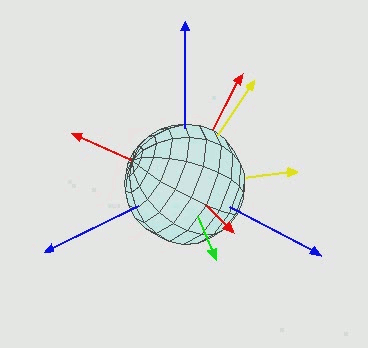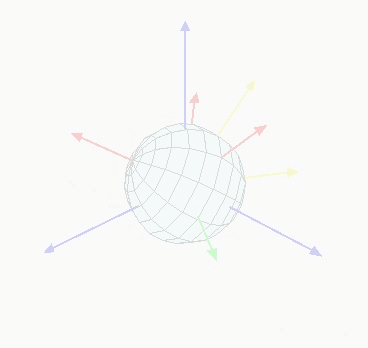
Notation
First of all, the sample frame coincides with one grain frame.
R is based on the sample frame. Normal direction (Z) cosine 001 in the sample frame, R * Z -> one grain 001 orientation (Z’) in the sample frame.
Inverse of R is based on the grain frame. One grain 001 orientation (z) in the grain frame, R-1 * z -> sample normal direction in the grain frame.
Normal direction in the Grain frame
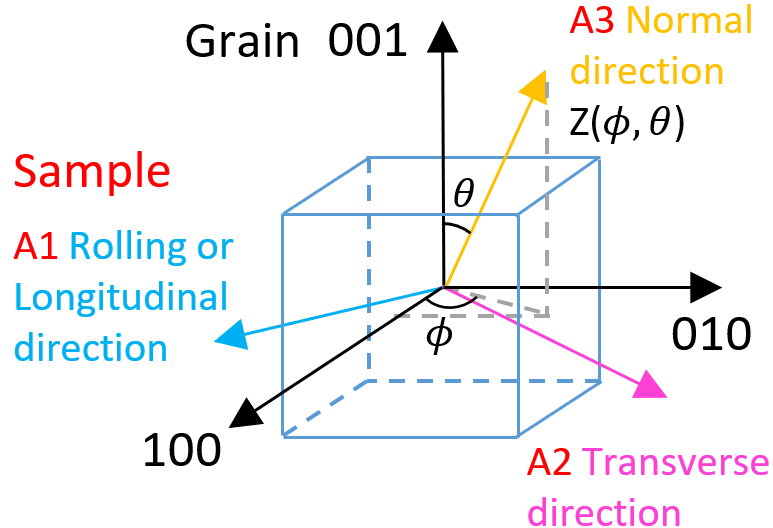
Sample frame Normal direction 001
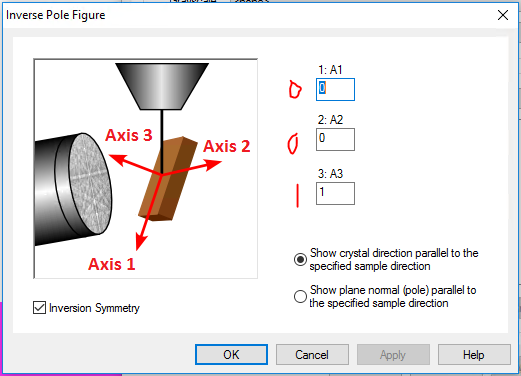
Sample frame Normal direction, Rolling direction and Transverse direction
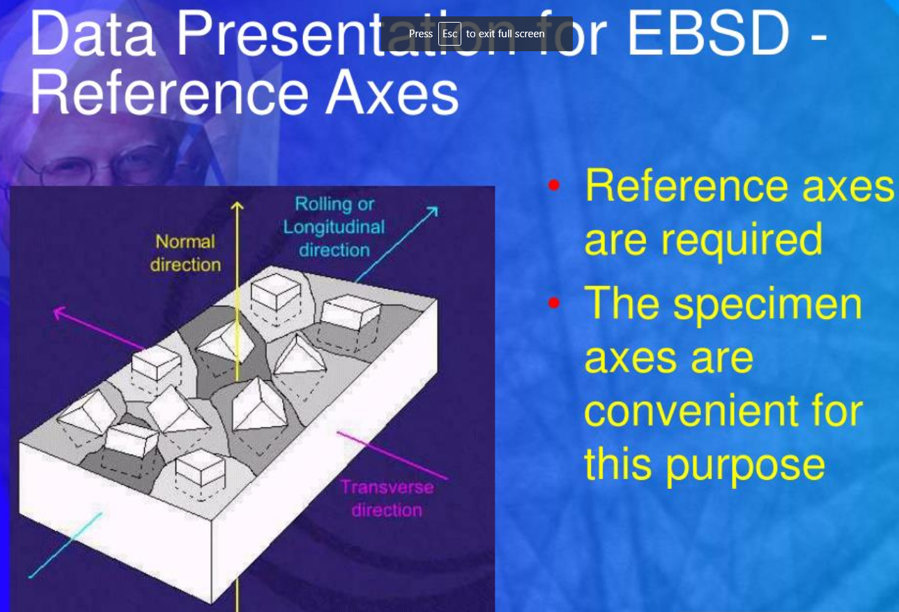
https://en.wikipedia.org/wiki/Euler_angles
http://solidmechanics.org/text/Chapter3_2/Chapter3_2.htm
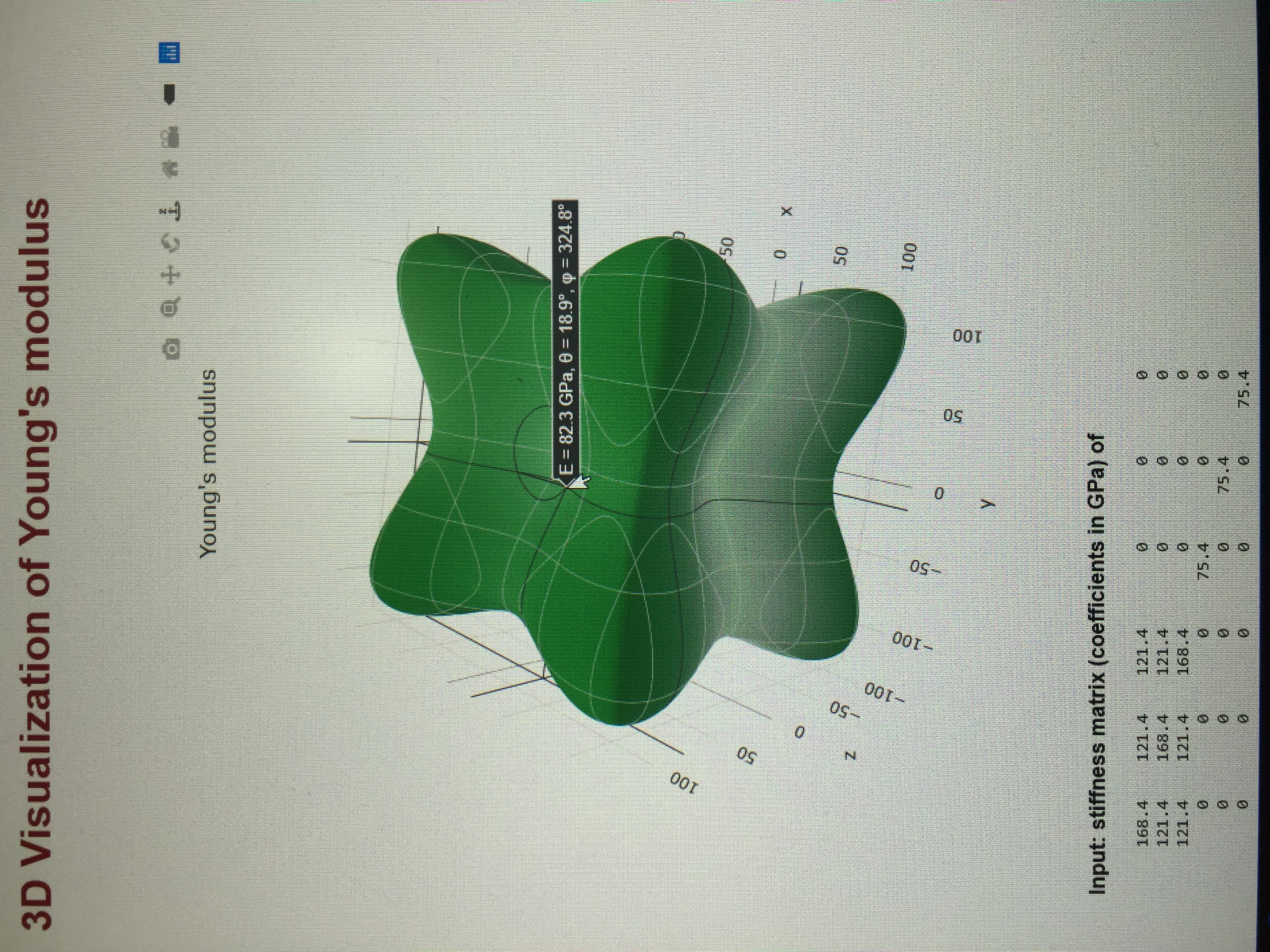
http://progs.coudert.name/elate
Input: stiffness matrix (coefficients in GPa) of Cu
168.4 121.4 121.4 0 0 0
121.4 168.4 121.4 0 0 0
121.4 121.4 168.4 0 0 0
0 0 0 75.4 0 0
0 0 0 0 75.4 0
0 0 0 0 0 75.4

https://www.wolframcloud.com/objects/zp2130/Published/IPF_Color_Map.nb