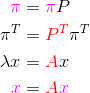Policy Gradient Methods
Policy Gradient Methods In summary, I guess because 1. policy (probability of action) has the style: , 2. obtain (or let’s say ‘math trick’) in the objective function ( i.e., value function )’s gradient equation to get an ‘Expectation’ form for : , assign ‘ln’ to policy before gradient for analysis convenience. pg Notation J(θ):… read more »