Author: Daniel Schury

Posted on

Cosmic Water

Where does water actually come from? Most people would say, from the tap. While this certainly is true, scientists are – fortunately I would say, unfortunately my significant other might say – not like most people. They want to know more.

Before answering this question we should step back and ask, what is water? Water is a molecule, H2O. That means it consists of one oxygen atom, O, and two hydrogen atoms, H2. One way to produce water is to mix hydrogen and oxygen and ignite it. While on earth this can easily be done, on a cosmic scale initiating the reaction is far more complex. The biggest problem is that cosmic space  is cold. Like, really cold. The official record for the coldest temperature measured on earth is held by the arctic Vostok Station with −128.6 °F (−89.2 °C). In comparison, diffuse dense clouds, common cosmic structures where a lot of cosmic chemistry happens, have temperatures of -441.7°F to -279.7°F (-263.2°C to -173.2°C).  Anybody who has ever tried to cook but forgot to turn on the stove knows that for chemistry to happen, heat often has to be supplied, like through the flame in the above experiment. So, how can chemistry happen in the coldness of space?

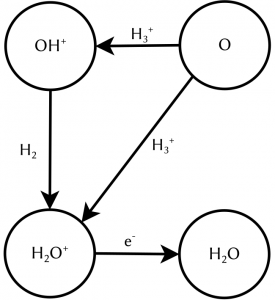
The key to understanding this lies in the state of matter of cosmic gas. On earth, matter is mostly electrically neutral. That means, it contains exactly the same number of positively and negatively charged particles which therefore cancel each other out. To electrostatically charge an object, we have to actively make an effort, think of rubbing a balloon against your hair. This is not true for the universe in general. Actually, most matter in space is not neutral but charged. One notable example is the molecular ion H3+, a molecule consisting of three hydrogen atoms which are missing one electron, leading to a singly positively charged ion. Charged molecules can undergo reactions which are not possible for their neutral counterparts. For example, they react at temperatures at which their neutral counterparts do not react. In chemistry charged molecules are called radicals and are widely known for having a bad influence on your health. So stay away from cosmic clouds to avoid wrinkles! One reaction network starts with the reaction of atomic oxygen O with H3+. In a first step, two outcomes are possible: either they react to OH+ and H2 which in a second step reacts to H2O+ which subsequently neutralises, or they directly react to H2O+ and H before undergoing the neutralisation. Until recently, little was known about which of the two outcomes was more likely. Therefore, astronomical modelling assumptions had to be made. A precise knowledge of the pathway of the reaction network shown in figure 1 is especially interesting for interstellar regions in which the interstellar OH+ can be destroyed before reacting to H2O+. Here the direct reaction is the only efficient way of forming water, since potentially every intermediate product can undergo reactions not resulting in H2O+, therefore less steps directly increase the reaction yield.

Fig. 1: A strongly simplified excerpt of the reaction network of oxygen resulting in water.
Fig. 1: A strongly simplified excerpt of the reaction network of oxygen resulting in water.

This gap of knowledge was filled by Hillenbrand and colleagues, who accurately measured the reaction O + H3+ for both possible outcomes and therefore were able to give the ratio between them. But wait, didn’t we just learn that for the cosmic area of interest, this reaction takes place at highly unpleasant freezing temperatures? How on earth can this be reproduced on earth in the laboratory while still being able to control the setup? For this, the scientists came up with a nice little trick. On a microscopic level, the temperature of an object can be linked to the velocity of the particles it is made up of. Hotter particles move faster, colder ones move slower. If packed densely together, they constantly hit each other and change their direction of movement, leading to a constant vibration of the whole particle cloud. And the stronger the vibrations, the hotter they are.

This phenomenon was first discovered in 1827 by the Scottish physicist Robert Brown and linked to their temperature in the PhD thesis of Albert Einstein in 1905. The scientists made use of this phenomenon to study the reaction with “cold” reactants without actually cooling them down. Instead of mixing gases of cold O and H3+ together, they created two directed particle beams and let them overlap so the reaction could take place. Even though the beams were produced at room temperature and their individual velocity was quite high, the velocities of the beams relative to each other could be controlled to be very small. Think of driving on the highway and passing another car: You may be travelling at a speed well above 60 mph, corresponding to over 5200 feet per minute. Still, it can actually take you multiple seconds to fully pass a vehicle 10 feet long or more if you are not driving much faster than it, therefore having a low relative speed. And as we just learned, a small velocity corresponds to a low temperature.

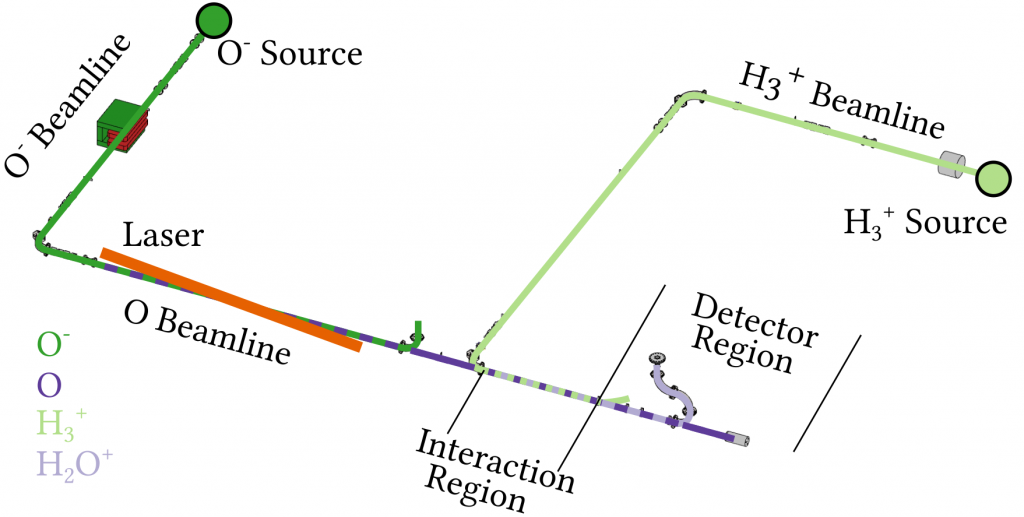
Fig. 2: The dual source merged beam setup to measure the O + H3+ reaction.
Fig. 2: The dual source merged beam setup to measure the O + H3+ reaction.

To study the reaction the scientists used the setup shown in figure 2. They used two ion sources to produce either a beam of H3+ or O- ions. Since the experiment requires neutral oxygen atoms, the negatively charged O- ions are first neutralised by a laser, which kicks away the additional electron. These two beams are then overlapped in an interaction region allowing the chemical reaction to take place. Varying the relative velocity of the beams, corresponding to varying the temperature at which the reaction takes place, it can be studied over a broad range of temperatures, ranging from close to absolute zero to more than 1000°F.

 

Using this setup they could measure the so-called branching ratio, meaning the ratio of the outcomes H2O+ to OH+, over a wide temperature range. For low temperatures they found a ratio close to 1:1, whereas for higher temperatures only 20% of the reactions resulted directly in H2O+. In astrochemical models over the whole temperature range a fixed ratio of 30:70 was used, originating from a single measurement at room temperature, which was found to be not true. This implies that the frequently used model underestimates the production of water in cold interstellar regions and has to be adapted.

Posted on

How Bouldering keeps urban communities in shape

So, you too enjoy this amazing sport, where people climb over comparatively short distances without any tools, such as ropes or harnesses? Amazing! But, to quote a famous British ensemble, now for something completely different. Today we want to talk about a more serious and urgent topic: flood risks. The recent flood in the New York City area convincingly showed us the risk of flooding in (highly) populated urban areas. Climate change and socioeconomic developments keep on increasing this risk further and further.

Flooding in NYC
Figure 1: Strong rain in New York City transformed parts of it into Venice’s little brother, with less romance but at least 43 death cases.

The United Nations have formulated in their 2030 Agenda for Sustainable Development 17 goals to »[…] stimulate action over the next fifteen years in areas of critical importance for humanity and the planet«. Goal number 11 is »sustainable cities and communities«. But, to properly address a risk it is necessary to adequately analyze and describe it. Current approaches for urban risk analysis mostly lack two important factors: First, they are mainly qualitative but not quantitative. That means, they accurately describe the what of a risk but not how much. We probably all can agree that the information that the biggest crocodile ever found in nature was longer than the biggest giraffe ever was high is much more impressive than the statement, crocodiles can become really big. This demonstrates why quantitative statements are important.

The second problem they do not address properly is the prediction of urban development. They project city growth rather arbitrarily, seldomly incorporating geographical, social or economic factors associated with urbanization. While predictions are difficult, especially about the future, some information exists which can be used as a guide about most probable development cases.

Dr. Mona Hemmati and colleagues tackled both these problems by developing a framework for understanding the interactions between urbanization and flood risks. To do so, they combined four main components: an urban growth module, a hazard module, a risk assessment module and a policy implementation module. The urban growth module is used to achieve a more realistic urban development prediction and the hazard module to generate floodplains. For the risk assessment module the two previous modules are combined while the policy implementation module is used to implement nonstructural strategies, such as for example development zones or taxation variations.

For the framework development the City of Boulder, Colorado, has been chosen as a testbed. Various data such as size, shape, surrounding area or density distribution of the city has been gathered by different sources and used as input parameters for their model.

Their urban growth model has four key features which are used to predict the urbanization process, divided into residential, industrial and commercial & mixed-used occupation. They divide the urban area and surroundings into equally sized cells, the so-called cell space, creating a 2D spatial grid. Each cell can have a cell state, which describes if the cell is developed or not. The neighbourhood of a cell is a factor which can either have an attractive or repulsive effect on the surrounding cells and the transition potential represents the probability of a cell state change for the next time step, defined by different development factors. For the hazard module a development by the Federal Emergency Management Agency was used. With this different floodplains characteristics can be calculated for various flood scenarios, such as for 5, 10, etc. year return period. The risk assessment module measures the damage to physical infrastructure and caused by economic and social disruptions as expected annual damage (EAD) in $US. Last, the policy implementation module takes into account nonstructural flood mitigation measures. Structural measures, such as for example dams, aim at controlling the hazard and keeping the flood out, while nonstructural measures, such as for example land acquisition or public awareness programmes aim at reducing the exposure to hazard.

Using this framework, they tested two different policies against both the current development policy of the city as well as no policy at all. For the first policy they defined low-risk zones and disallowed development and high-risk zones, while for the second they defined socioeconomic incentives, such as for example placing school and places of entertainment in low-risk zones. The interesting result was, that from the four tested cases, Boulder’s current development policy showed the worst result in terms of growth inside the floodplains and therefore long-term costs. Even uncontrolled development was better, while the best policy was the zoning policy, closely followed by the incentive policy.

It can be summarised that while their model still contained many educated guesses and assumptions and for example neglected the influence of the growth module onto the hazard module it can be considered a huge step forward in comparison to purely qualitative models based on random development. The testbed Boulder showed it can be directly applied to community planners in assisting the mitigation of risks due to future hazards, bringing the science out of their ivory tower into the heart of modern society: The city itself.

Dr. Mona Hemmati is a Postdoctoral Research Scientist in the department for Ocean and Climate Physics at the Lamont-Doherty Earth Observatory (LDEO) of Columbia University.

Posted on

Shedding light on transfers in soccer – from a physicist’s point of view

Ever wondered about the connection between sports, architecture and molecular physics? These three distinctive fields come together when we talk about fullerenes. Fullerenes are a modification of carbon with some very interesting properties. The most outstanding one is their structure: They are hollow spheres made up of several penta- and hexagons, resembling a cage. The most famous fullerene C60 (Fig. 1a) actually looks very similar to the traditional pattern of a soccer ball (Fig. 1b). Fullerenes are named after the American architect Richard Buckminster Fuller who is famous for his constructions of geodesic domes, very similar to the fullerenes structure (Fig. 1c). Therefore fullerenes are commonly referred to as Buckminster Fullerenes or Bucky Balls. Fullerenes can build a unique molecular structure where atoms, molecules or even other small clusters are bound inside of the cage. These molecules are called endohedral molecules, with Ho3N@C80 (Fig. 1d) being an example introduced later in this text.

3D structure of fullerenes in comparison with a soccer ball and a geodesic dome
a) The carbon cage structure (grey) of C60 with the typical pentagons (orange) and hexagons (purple). b) The same structure can also be found in a classical design of a soccer ball. c) The Biosphère in Montreal, designed by R. B. Buckminster. d) The molecule used in the study, Ho3N@C80.

Endohedral molecules have gained some attention in biochemical research for two reasons. First, they are considered excellent vehicles to transport drug molecules to specific locations and release the cage’s content by an externally triggered mechanism. Second, they could be applied in radiotherapy, since the ability to carry metal atoms inside allows them to release a large amount of electrons which cause very localised cell damage, especially to cancer cells.

One mechanism which is expected to play an important role for these two applications is the so-called intermolecular coulombic decay (ICD, not to be confused with the International Classification of Diseases). In an atom, electrons are bound to the nucleus in so-called shells which layer above each other like an onion (a property they share with ogres). To remove an electron from its shell one has to supply energy to it, the closer to the nucleus the shell is, the more energy is needed. A common way of supplying this energy is to shine high-energetic light onto the atoms, either ultraviolet (UV) or even X-rays. If an electron is removed from an atom, we call the remaining atom an ion. If an inner electron is removed, a vacancy or “free spot” in that shell is created. Such ions are called excited.

Speaking from personal experience, excitement tends to decay quickly (citation needed), which also holds true for ions. Within an ion, an electron from a higher shell “falls down” (decays) into the vacancy of the inner shell. By doing so it has to give up the difference in energy between the two shells. One way to give up its energy is by emitting a photon, meaning shining light. This effect is used for example in neon bulbs. If the two involved shells are far enough from each other, the electron can transfer its energy to another electron which is then removed from its shell. This process is called the Auger effect (Fig. 2a). Within molecules another process can happen: The decaying electron can transfer its energy onto an electron of another atom in the molecule which then gets removed from its shell (Fig. 2b). This is the aforementioned ICD.

scheme of the auger effect and ICD in molecules and endohedral fullerenes
a) Schematic of the Auger effect. b) ICD in a normal molecule. c) ICD in an endohedral molecule.

Unfortunately, ICD in endohedral molecules (Fig. 2c) has, even though theoretically predicted, not been discovered. Well, until recently. Dr. Razib Obaid and colleagues set up an experiment at the Advanced Light Source (ALS) in Berkeley, one of the world’s brightest UV and X-ray light source facilities in the world. They used the UV light to radiate the molecule Ho3N@C80 (a molecule consisting of three holmium and one nitrogen atom, trapped in a cage of 80 carbon atoms). The result was the production of ions and electrons, which the researchers measured together with their energy distribution. Additionally, they measured the relation of the particle’s production time. Putting these measurements together, they were able for the first time to demonstrate ICD in endohedral molecules. This required not only a clever experimental setup, but also a lot of theoretical effort. The complexity of the experiment and its analysis derives from the fact that ICD involves multiple atoms with many electrons. This makes the measured spectra resulting from  such experiments difficult to disentangle and complicates the assignment of each individual process.

With the first clear observation of ICD in endohedral fullerenes, demonstrating the existence of the proposed mechanism, the researchers have opened the door to further research on the application of the process as a drug delivery system and its influence in the propagation of radiation induced molecular damage in biomolecules.

Dr. Razib Obaid is currently a postdoc at RARAF Radiological Research Accelerator Facility located at the Nevis Laboratory of Columbia University, lead by Dr. David J. Brenner.

Images:

Figure 1b: Derived from Football (soccer ball).svg. (2020, September 23). Wikimedia Commons. Retrieved 23:10, August 30, 2021

Figure 1c: Biosphere, Montreal.jpg. (2020, October 26). Wikimedia Commons,. Retrieved 23:11, August 30, 2021

Posted on

Random Walking – When having no clue where to go still makes you reach your destination

In empirical sciences, theories can be sorted into three categories with ascending gain of knowledge: empirical, semi-empirical and ab initio. Their difference can best be explained by an example: In astronomy the movement of all planets was known since ancient times. By pure observation astronomers could predict where in the sky a certain planet would be at a given time. They had the knowledge of how they moved but actually no clue why they did so. Their knowledge was purely empirical, meaning purely based on observation. Kepler became the first to develop a model by postulating that the sun is the center of the planetary system and the planet’s movement is controlled by her. Since Kepler could not explain why the planets would be moved by the sun, he had to introduce free parameters which he varied until the prediction of the model matched the observations. This is a so-called semi-empirical model. But it was not until Newton who with his theory of gravity could predict the planets movements without any free parameters or assumptions but purely by an ab initio, latin for “from the beginning”, theory based on fundamental principles of nature, namely gravity. As scientists are quite curious creatures, they always want to know not only how things work but also why they work this way. Therefore, developing ab initio theories is the holy grail in every discipline.

Luckily, in quantum mechanics the process of finding ab initio theories has been strongly formalized. This means that if we want to know the property of a system, for example its velocity, we just have to kindly ask the system for it. This is done by applying a tool, the so-called operator, belonging to the property of interest on the function describing the system’s current state. The result of this operation is the property we are interested in. Think of a pot of water. We want to know its temperature? We use a tool to measure temperature, a thermometer. We want to know its weight? We use the tool to measure its weight, a scale. An operator is a mathematical tool which transforms mathematical functions and provides us with the functions property connected to the operator. Think of the integral sign which is an operator too. The integral is just the operator of the area under a function and the x-axis.

The problem is, how do we know the above mentioned function describing the system’s state? Fortunately, smart people developed a generic way to answer this problem too: We have to solve the so-called Schrödinger equation. Writing down this equation is comparably easy, we just need to know the potentials of all forces acting on the system and we can solve it. Well, if we can solve it. It can be shown that analytical solutions, that means solutions which can be expressed by a closed mathematical expression, only exist for very simple systems, if at all. For everything else numerical approaches have to be applied. While they still converge towards the exact solution, this takes a lot of computational time. The higher the complexity of the system, the more time it takes. So for complex systems even the exact numerical approach quickly becomes impractical to use. One way out of this misery is simplification. With clever assumptions about the system, based on its observation one can drastically reduce the complexity of the calculations. With this approach, we are able to, within reasonable time, find solutions for the problem which are not exact, but exact within a certain error range.

Another way to find a solution for these complex problems is getting help from one of nature’s most powerful and mysterious principles: chance. The problem of the numerical exact solving approach is that it has to walk through an immensely huge multidimensional space, spanned by the combinations of all possible interactions between all involved particles. Think billions of trillions times billions of trillions. By using a technique called Random Walking the time to explore this space can be significantly reduced. Again, let’s take an example: Imagine we want to know how many trees grow in a forest. The exact solution would be dividing the forest into a grid of e.g., 1 square foot, and counting how many trees are in each square. A random walk would start in the forest center. Then we randomly choose a direction and a distance to walk before counting the trees in the resulting square. If we repeat this just long enough we eventually will have visited every square, therefore knowing the exact number, meaning the random walk converges towards the exact result. By having many people starting together and doing individual random walks stopping when their results deviation is below a certain threshold a quite accurate approximation can be obtained in little time.

Columbia postdoc Benjamin Rudshteyn and his colleagues developed a very efficient algorithm based on this method specifically tailored for calculating molecules containing transition metals such as copper, niobium or gold. While being ubiquitous in biology and chemistry, and playing a central role in important fields such as the development of new drugs or high-temperature superconductors, these molecules are difficult to treat both experimentally and theoretically due to their complex electronic structures. They tested their method by calculating for a collection of 34 tetrahedral, square planar, and octahedral 3D metal-containing complexes the energy needed to dissociate a part of the molecule from the rest. For this, precise knowledge of the energy states of both the initial molecule and the products is needed. By comparing their results with precise experimental data and results of conventional theoretical methods they could show that their method results in at least two times increased accuracy as well as increased robustness, meaning little variation in the statistical uncertainty between the different complexes.

molecule complex geometries
Figure 1: Illustration of the three types of geometry of the datasets molecules: Octahedral (a), square planar (b) and tetrahedral (c), with the transition metal being the central sphere. In (d) the dissociation of part of the molecule is shown.

While still requiring the computational power of modern supercomputers, their findings push the boundaries of the size of transition metal containing molecules for which reliable theoretical data can be produced. These results can then be used as an input to train methods using approximations to further reduce the computational time needed for the calculations.

Dr. Benjamin Rudshteyn is currently a postdoc in the Friesner Group of Theoretical Chemistry, lead by Prof. Dr. Richard A. Friesner, in the Department of Biological Sciences at Columbia University.

Follow this blog

Get every new post delivered right to your inbox.